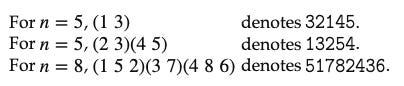Permutations: Cycles and Transpositions
[This is a preview of the full article.]
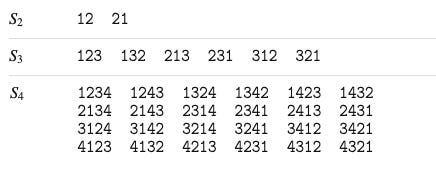
This is a collection of notes about permutations — all the different ways of ordering a set of distinct elements. In group theory, the group of permutations of size n is denoted S_n. For example:
You can think of a single permutation as either a particular ordering of the integers 1 through n, or, equivalently, as a 1-1 and onto mapping f:{1,…,n}→{1,…,n}. There’s a natural way to write such a mapping f, which is to list out f(1),f(2),…,f(n) as a string; you can consider the lists of elements of S_2, S_3, and S_4 above to be in this string notation. By default, this article will view permutations as mappings.
This article covers the following independent observations about permutations:
I’ll introduce the idea of a cut-merge operation, and show how this corresponds to a transposition; a transposition is a permutation that exchanges two elements of a set, and changes no others. Given the set {1, 2, 3, 4, 5}, the swap of 2 and 5 would be a transposition; I might write this permutation as
15342.Permutations can be split into two kinds: odd permutations and even permutations. Just as odd + even = odd when it comes to integer addition, the analogous rules hold for permutations under composition. For example, if I apply an odd permutation, and then apply an even permutation after that, the result of the combined permutations is itself an odd permutation (and this analogy holds for all combinations of odd/even). I’ll present a simple proof of this breakdown using cut-merge operations.
I’ll discuss a generalization of the parity (even-ness or odd-ness) of a permutation π that I call the magnitude m(π) of the permutation.
I’ll define the cycle structure 𝖼𝗌(π), which captures the sizes of cycles in the permutation π; and I’ll show that 𝖼𝗌(a⋅b)=𝖼𝗌(b⋅a) for any two permutations a,b.
I’ll show that the magnitude m(⋅) acts like a norm on the group S_n, and that it can define a coherent distance function 𝖽𝗂𝗌𝗍(⋅,⋅) on S_n.
When I say these are independent observations, I mean that these ideas are new to me. I have not tried much to check if they are new to the world altogether — in all likelihood, many of these ideas have been discovered by others before me. Still, I think they’re fun ideas worth sharing.
1 Cycle Notation
Any permutation is a specific ordering of a set of distinct elements. This article focuses on finite permutations, and I’ll generally use the variable n to denote the size of the set being permuted. It’s simple and traditional to think of a permutation as a bijection (a 1-1 and onto mapping) of the first n integers — for example, here’s a permutation of the set {1,2,…,8} in string notation:
π = 15273648. (1)
Despite the possible confusion with the constant π = 3.141…, it’s also traditional to use the variable π for a permutation, as (clearly) π stands for “πermutation.”
There are many fun ways to denote or think about a particular permutation. For example, given π as in (1), we could think of it as the sequence π_1=1, π_2=5, …, π_8=8. We could also think of it as a function π:[n]→[n], using [n] to denote the integers {1,2,…,n}.
This article uses a particular notation for permutations called cycle notation: the idea for cycle notation is to write out a string of integers in [n] with the interpretation that any consecutive pair ij indicates that i is mapped to j, and any i at the end of a parenthesized group maps to j at the start of the same group. Our permutation from (1) looks like this in cycle notation:
π = (253)(47)
because π(2)=5, π(5)=3, and π(4)=7. Each sequence in parentheses wraps around, so π(3)=2 and π(7)=4. Thus each parenthesized sequence is a cycle. It is understood that any omitted elements are mapped to themselves; since π(1)=1, we don’t need to include 1 in the cycle notation for π.
Examples:
You could write the same permutation many ways in cycle notation; for example:
π = (74)(532) = (325)(74) = (253)(47).
Among those choices, I consider the last one to be standard because it’s lexicographically first.
Read the rest of this article on my homepage!