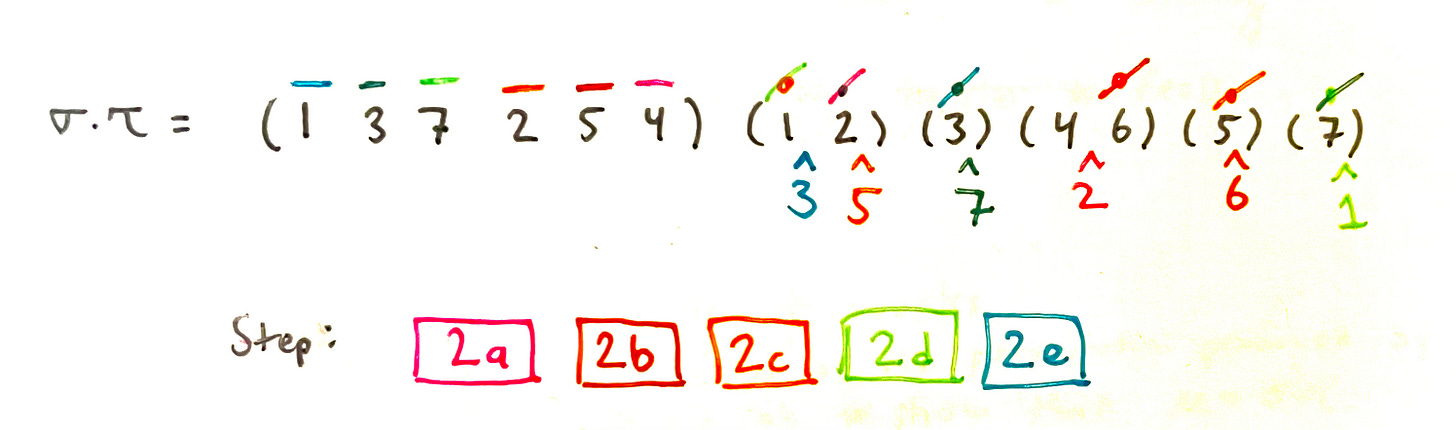Permutations: A Chalkboard Algorithm

[This is a preview of the full article.]

This short article describes a chalkboard method for multiplying (that is, composing) permutations written in cycle notation. When I call it a chalkboard method, I mean that it’s useful for humans doing simple math by hand — akin to long-hand addition taught in school — and as opposed to an algorithm designed for a computer.

This article can be read as an extension to an earlier note about permutations, although this one can be read independently, assuming that you know both what permutation multiplication (synonymously, composition) is, and what cycle notation is. (If not, you can learn by reading the previous note in this series.)

The chalkboard algorithm I’ll describe is something I derived for fun. I haven’t put effort into discovering if someone else has come up with it before me.

Let’s get started. As an example, consider

σ = (1 3 7 2 5 4) and τ = (1 2)(4 6).

We can define the product σ⋅τ as the permutation μ where

μ(x) = (σ⋅τ)(x) = τ(σ(x)). (2)

I’ve chosen to work with the intuition that the element on the left (σ) “happens first;” this notation seems more natural to me. Some authors choose the opposite ordering because it avoids the awkward reversal of symbols in (2).

In our example,

μ = (1 3 7)(2 5 6 4),

as can be verified by asking, for each x∈{1, 2, …, 7}, what is y = σ(x)? followed by asking what is τ(y)?

Let’s informally call this a 2-lookup method, in the sense that a human will perform a scan of σ to find σ(x) and then another scan of τ to find τ(y) for each input x to μ. This article improves on this by providing an algorithm that is a 1-lookup method. In some informal sense we can say it’s twice as fast for a human to execute.

A computer can multiply permutations even more efficiently. We could encode a permutation as a hash map (a dict in Python, or an object in JavaScript, for example) where the keys are the input numbers and the values are what those values map to. In this case, each lookup of a value μ(x) takes constant time, so that computing all of μ requires O(n) time, where n is the size of the domain of the permutations. I don’t consider a human working on a chalkboard to have access to constant-time lookups, so this algorithm is only for computers.

Read the rest of this article on my homepage!